Question

Fully Factor the following expression: 3a2 – 9a - 30

Answer 1

`3a^2-9a-30​`

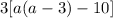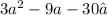
Notice that all the terms are divisible by 3. First we factor out 3.

`\begin{gathered} 3a2-9a-30​ \\ 3(a^2-3a-10) \end{gathered}`

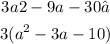
Also, the first two terms has a in it. We can factor out a.

`\begin{gathered} 3(a^2-3a-10) \\ 3\lbrack a(a^{}-3)-10\rbrack \end{gathered}`

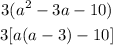
Notice that we use the square bracket to indicate the distribution of the first factor which is 3, and the parenthesis indicates the distribution of the second factor a which only apply to the first two terms.

Answer:

`3\lbrack a(a^{}-3)-10\rbrack`