Question

Using the Binomial distribution,If n=10 and p=0.2, find P(x=5). Round your answer to three decimal places.

Answer 1

Step-by-step explanation

To solve this problem, we will use the formula for the probability of the Binomial distribution:

`b(x;n,p)=(n!)/((n-x)!\cdot x!)\cdot p^x\cdot(1-p)^(n-x).`

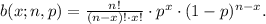
Where:

• b(x; n, p) = the binomial probability for x,

,

• x = the total number of successes,

,

• n = the number of trials,

,

• p = the probability of success on an individual trial.

From the statement, we know that:

• x = 5,

,

• n = 10,

,

• p = 0.2.

Replacing these data in the formula above, we get:

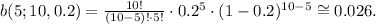
`b(5;10,0.2)=(10!)/((10-5)!\cdot5!)\cdot0.2^5\cdot(1-0.2)^(10-5)\cong0.026.`Answer

0.026