Question

A baby girl weighs on average 7 pounds when she is born with standard deviation of 1.23 pounds assume the weights of baby girls are normally distributed sketch a picture of this graph be sure to graph and label the mean and 3 standard deviations left and right of the mean b. Jessica and her friend Maria give birth on the same day. Jessica daughter weigh 5.4 pounds Maria daughter weigh 9.8 pound locate Jessica and Maria daughter on the curve above estimate their z values

Answer 1

We know that

• The average is 7 pounds.

,

• The standard deviation is 1.23 pounds.

To label 3 standard deviations on the right, we have to add them to the mean. To label 3 standard deviations on the left, we have to subtract from the mean.

Right.

`\begin{gathered} 7+1.23=8.23 \\ 8.23+1.23=9.46 \\ 9.46+1.23=10.69 \end{gathered}`

Left.

`\begin{gathered} 7-1.23=5.77 \\ 5.77-1.23=4.54 \\ 4.54-1.23=3.31 \end{gathered}`

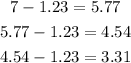
Let's sketch the graph

Let's find Jessica's and Maria's z-score.

`\begin{gathered} Z_{\text{Jessica}}=(x-\mu)/(\sigma)=(5.4-7)/(1.23)=(-1.6)/(1.23)=-1.3_{} \\ Z_{\text{Maria}}=(x-\mu)/(\sigma)=(9.8-7)/(1.23)=(2.8)/(1.23)=2.3 \end{gathered}`

Maria's daughter's weight could be considered an outlier because it's far away from the mean of 7 pounds.

So, we should be concerned about Maria's daughter because her way is too high.