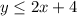
We will substitute x by the x-coordinate of the given point and check the value of y
At x = 0
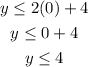
The value of y = 6
and 6 not smaller than or equal 4
(0, 6) not a solution
At x = 2

The value of y is 3
3 is smaller than 8
(2, 3) is a solution to the inequality
Let us check the other points
At x = -4
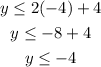
The value of y is 1
1 is not smaller than -4
(-4, 1) not a solution to the inequality
At x = 0
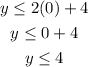
The value of y = 4
4 is equal to 4
(0, 4) is a solution to the inequality also
Ok
Because they need different answers we can not put then in one session
So you should to