Answer:
m∠T= 45°
Explanation:
In a parallelogram, consecutive (or adjacent) angles add up to 180 degrees.
In parallelogram MNTU, angles T and U are consecutive angles, therefore:
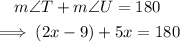
First, solve the equation for x:
![\begin{gathered} 2x-9+5x=180\degree \\ \text{ Add 9 to both sides of the equation} \\ 2x-9+9+5x=180\operatorname{\degree}+9 \\ 7x=189 \\ \text{ Divide both sides by 7} \\ (7x)/(7)=(189)/(7) \\ x=27\degree \end{gathered}]()
Therefore:
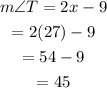
The measure of angle T is 45 degrees.