Question

A circle has a radius of 4/9 units and is centered at(-6.2,5.8) write the equation

Answer 1

Step 1: Write out the formula

`(x-a)^2+(y-b)^2=r^2`
`\begin{gathered} \text{ Where} \\ a=\text{ the x-coordinate of the center} \\ b=\text{ the y-coordinate of the center} \\ r=\text{ the radius of the circle} \end{gathered}`

Step 2: Write out the given values and substitute them into the equations

In this case,

`a=-6.2,b=5.8,r=(4)/(9)`

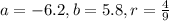
Therefore, the equation of the circle is given by

`\begin{gathered} (x-(-6.2))^2+(y-5.8)^2=((4)/(9))^2 \\ \text{ this implies that} \\ (x+6.2)^2+(y-5.8_{})^2=(16)/(81) \end{gathered}`

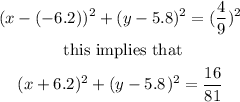
Since, (x + a)² = x² +2ax + a² and (y - b)² = y² - 2by + b², then

`x^2+2(6.2)x+(6.2)^2+y^2-2(5.8)y+(5.8)^2=(16)/(81)`
`x^2+12.4x+y^2-11.6y+38.44+33.64=(16)/(81)`
`x^2+12.4x+y^2-11.6y+38.44+33.64-(16)/(81)=0`
`x^2+12.4x+y^2-11.6y+71.8825=0`

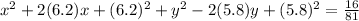
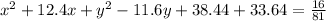
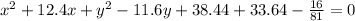
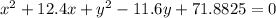
Hence, the equation is (x + 6.2)² + (y - 5.8)-