The binomial theorem says that
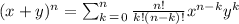
Looking at our problem we can see that
• x = 4t
,
• y = -3
,
• n = 5
Using it in the binomial theorem
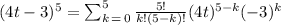
And now we do the calculus for each term, then, I'll do it separated, just to be organized since binomial theorem calculus can be long, I'll start with k = 0 and go on.
k = 0
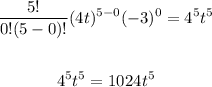
k = 1
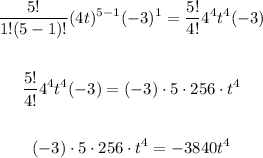
k = 2
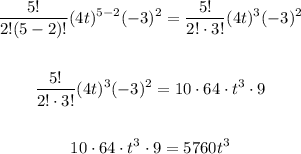
k = 3
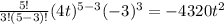
k = 4
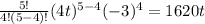
And the last one, k = 5
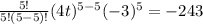
Now we did all terms, the binomial will be the sum of all of them
