Question

A crossbow will come partially sighted in, This takes into account that the arrow fall asit moves towards its target. If l were to shoot he bow horzontalify it would hit well below inhertarget. Given that I practice from 30.0 meters away from the target and the crossbow launches the arrows at a total velocity of 110.0 m/s. If the shot Was setup to launch exactly horizontally and the bow was pointed at the bullseye. How far below the bullseye will the arrow hit?

Answer 1

Given,

The range of the flight of the arrow, R=30.0 m

The initial launch velocity of the arrow, u=110.0 m

It is given that the arrow is launched horizontally, thus the vertical component of the launch velocity of the arrow is 0 m/s.

The range of the flight of the arrow is given by,

`R=(u)/(t)`

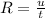
Where t is the time of flight of the arrow.

On substituting the known values,

`\begin{gathered} 30.0=(110.0)/(t) \\ \Rightarrow t=(110.0)/(30.0) \\ =3.67\text{ s} \end{gathered}`

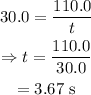
From the equation of motion, the drop in the height of the arrow during its entire is given by,

`h=u_yt+(1)/(2)gt^2`

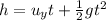
Where g is the acceleration due to gravity and u_y is the vertical component of the initial velocity of the arrow.

On substituting the known values,

`\begin{gathered} h=0+(1)/(2)*9.8*3.67^2 \\ =66\text{ m} \end{gathered}`

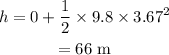
Thus the arrow will hit 66 m below the bullseye.