Question

A group fitness gym classifies class attendees by class type and member status the marketing team has gathered data from a random month in which there 2400 class attendees what is the probability that an attendee does not attend a boot camp

Answer 1

Probability is defined as the measurement of the likelihood of an outcome. It is mathematically expressed as:

`P=\frac{no\text{ of selected outcome}}{no\text{ of total outcomes}}`

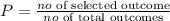
The selected outcome here is the number of members classified under boot camp.

`\text{ No of bootcamp members = }238\text{ + 283=521}`

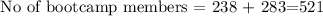
The probability of attending the boot camp therefore is:

`P=(521)/(2400)=0.2171`

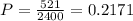
We know from probability that:

`\begin{gathered} P+Q=1 \\ \text{ Where} \\ Q\text{ = probability of non occurence of P} \end{gathered}`

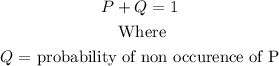
The probability of non-attendance of the boot camp therefore is:

`Q=1-(521)/(2400)=0.7829`

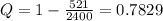
The probability that an attendee does not attend a boot camp is 0.7829