We know that
• Dan wants to use 200 feet maximum.
,
• He wants to make it in rectangular form with the length being four more than twice the width.
Based on the given details, we can for the following equation for the perimeter.

The perimeter is defined as
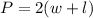
Replacing the first expression, we have
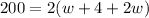
We solve for w

Now, we subtract 4 on each side

At last, we divide the equation by 3

Therefore, the width of the pin is 32 feet long.