Step-by-step explanation
Part 1
The cone shown is oblique. The formula to find the volume of an oblique cone and a right cone is the same. That formula is:
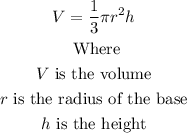
In this case, we have:
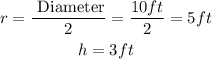
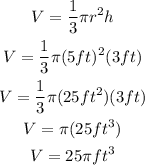
Part 2
Using a calculator, we multiply 25 by π and round to the nearest whole number.
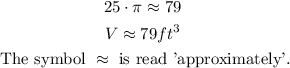
Answer
Part 1. The volume of the cone in terms of π is 25π cubic ft.
Part 2. The volume rounded to the nearest cubic foot is about 79 cubic ft.