Question

Find the average rate of change of the function from x = 1 to x = 2.F (x) = - 14/ x squared (x2)

Answer 1

Given the function f(x) defined as:

`f(x)=-(14)/(x^2)`

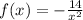
In general, to find the average rate of change of the function from x = a and x = b (a < b), we use the formula:

`Av=(f(b)-f(a))/(b-a)`

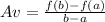
For this problem, a = 1 and b = 2. Then, we calculate f(1) and f(2) first:

`\begin{gathered} f(1)=-(14)/(1^2)=-14 \\ f(2)=-(14)/(2^2)=-3.5 \end{gathered}`

Finally, using the formula for the average rate of change:

`Av=(-3.5-(-14))/(2-1)=(-3.5+14)/(1)=10.5`