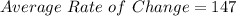Question

Describe how to determine the average rate of change between x=3 and x=5 for the function f(x) 3x^3+2 Include the average rate of change in your answer.

Answer 1

Given the function:

`f\mleft(x\mright)=3x^3+2`

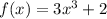
You can use the following formula to find the Average Rate of Change:

`Average\text{ }Rate\text{ }of\text{ }Change=(f(b)-f(a))/(b-a)`

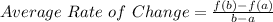
Where the following are two points on the function:

`\begin{gathered} (a,f(a)) \\ \\ (b,f(b)) \end{gathered}`

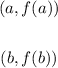
1. You know that you must determine the Average Rate of Change between:

`x=3\text{ and }x=5`

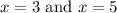
Then, you can set up that:

`\begin{gathered} a=3 \\ b=5 \end{gathered}`

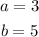
2. In order to find the corresponding value for:

`\begin{gathered} f(a)=f(3) \\ f(b)=f(5) \end{gathered}`

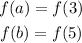
You can follow these steps:

- Substitute the value of "a" into the function and evaluate:

`f(3)=3(3)^3+2=3(27)+2=81+2=83`

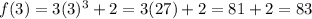
- Substitute the value of "b" into the function and then evaluate:

`f(5)=3(5)^3+2=3(125)+2=377`

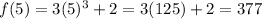
3. Knowing all the values, you can substitute into the formula for calculating the Average Rate of Change and evaluate:

`Average\text{ }Rate\text{ }of\text{ }Change=(377-83)/(5-3)=(294)/(2)=147`

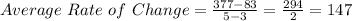
Hence, the answer is:

You can determine the average rate of change by finding the corresponding output values (y-values) for:

`x=3\text{ and }x=5`

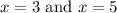
After finding those values, you can substitute them into the formula for calculating the Average Rate of Change, and then evaluate. It is:

`Average\text{ }Rate\text{ }of\text{ }Change=147`