Answer:
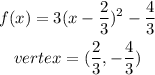
Explanations:
Given the quadratic equation expressed as:
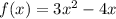
Factor out 3 from the expression
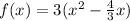
Complete the square of the expression in bracket
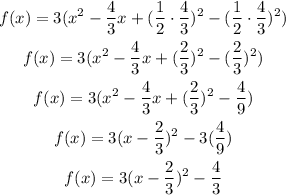
Since the vertex form of a quadratic equation is in the form f(x) = a(x-h)^2+k where (h, k) is the vertex.The vertex of the resulting function is (2/3, -4/3)