Question

Factor this polynomial completely using GCF then other quadratic methods. Then, find all x-intercepts of the polynomial as a function. 2x^3 +10x^2-28x

Answer 1

We have to factorize the polynomial:

`2x^3+10x^2-28x`

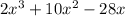
using the gratest common factor (GFC).

Then, we have to find all x-intercepts of the polynomial.

We can factorize each term as:

`\begin{gathered} 2x^3=2\cdot x^3 \\ 10x^2=2\cdot5\cdot x^2 \\ 28x=2\cdot2\cdot7\cdot x=2^2\cdot7\cdot x \end{gathered}`

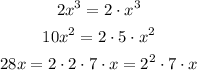
We have 2 and x as common factors of the polynomial, so we write:

`\begin{gathered} 2x^3+10x^2-28x \\ 2x(x^2)+2x(5x)-2x(2\cdot7) \\ 2x(x^2+5x-14) \end{gathered}`

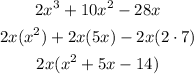
We now need to apply the quadratic formula to find the roots of the quadratic polynomial in parenthesis:

`\begin{gathered} x^2+5x-14 \\ \Rightarrow x=\frac{-5\pm\sqrt[]{5^2-4\cdot1\cdot(-14)}}{2\cdot1} \\ x=\frac{-5\pm\sqrt[]{25+56}}{2} \\ x=\frac{-5\pm\sqrt[]{81}}{2} \\ x=(-5\pm9)/(2) \\ x_1=(-5-9)/(2)=(-14)/(2)=-7 \\ x_2=(-5+9)/(2)=(4)/(2)=2 \end{gathered}`

We can now factorize the polynomial as:

`x(x^2+5x-14)=x(x+7)(x-2)`

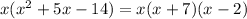
This factorized form gives us the x-intercepts:

`\begin{gathered} f(x)=0 \\ x(x+7)(x-2)=0 \\ \Rightarrow x_1=0 \\ x_2=-7 \\ x_3=2 \end{gathered}`

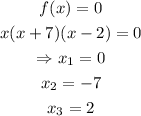
Answer:

The factorized polynomial is x(x+7)(x-2).

The x-intercepts are x = 0, x = -7 and x =2.