Question

AB = 4x + 6 and BC = 7x + 15. if AC = 120, find the length of segment AB.

Answer 1

To be able to find the length of segment AB, we'll need to find the value of the variable x;

So let's go ahead and determine what x is;

If we have a straight line drawn from point A to point C with point B being between them, then the below is true;

`AB+BC=AC`

Let's go ahead and substitute the given values for AB, BC and AC;

`\begin{gathered} AB+BC=AC \\ 4x+6+(7x+15)=120 \end{gathered}`

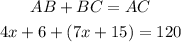
Solving fo x, we'll have;

`\begin{gathered} 11x+21=120 \\ 11x=99 \\ \therefore x=9 \end{gathered}`

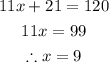
Let's go ahead and find the length of segment AB;

`\begin{gathered} AB=4x+6 \\ \text{But x = 9} \\ AB=4(9)+6 \\ =36+6 \\ =42 \end{gathered}`

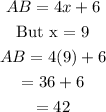
Therefore, the length of segment AB is 42.