Question

2. ** Find the coordinate point that makes both equations true. y = -5x + 3 2x - y = -3

Answer 1

Given the equations

`y=-5x+3`

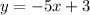
and

`2x-y=-3`

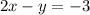
To determine the point where both equations are true, which means, where both lines intersect. You can use the substitution method.

This method implies writing one of the equations in terms of one of the variables and then replacing the obtained expression into the second equation. This way you use both equations to create a third one with only one variable.

The first equation is written for y, so we can substitute it directly into the second equation:

`\begin{gathered} 2x-y=-3 \\ 2x-(-5x+3)=-3 \end{gathered}`

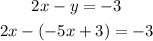
Take out the parentheses and simplify the like terms

`\begin{gathered} 2x+5x-3=-3 \\ 7x-3=-3 \end{gathered}`

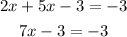
Pass "-3" to the right side of the equation by applying the opposite operation to both sides of the equal sign

`\begin{gathered} 7x-3+3=-3+3 \\ 7x=0 \end{gathered}`

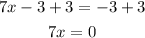
And divide both sides by 7

`\begin{gathered} (7x)/(7)=(0)/(7) \\ x=0 \end{gathered}`

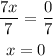
Now that we determined the value of x, replace it into the first equation to calculate the value of y:

`\begin{gathered} y=-5x+3 \\ y=-5\cdot0+3 \\ y=3 \end{gathered}`

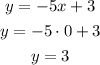
So the point where both equations are true, which means, where both lines intersect, is (0,3)