1 Answer

William Seiti Mizuta · Answer 1 · 2023-06-23T05:55:30+0000

We have to find the measure of ∠3.

We can use the fact that the sum of the measures of a triangle is equal to 180°.

Angles 1 and 2 are angles of the triangle. The last angle is the one that is supplementary to ∠3, so it can be expressed as (180° - ∠3).

Then, if we add the three angles of the triangle, we can write:

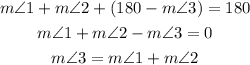
$\begin{gathered} m\angle1+m\angle2+(180\degree-m\angle3)=180\degree \\ m\angle1+m\angle2-m\angle3=0 \\ m\angle3=m\angle1+m\angle2 \end{gathered}$

Then, we can use this expression to find the value of x by replacing each angle by the expression given:

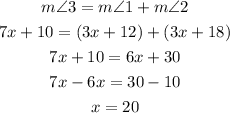
$\begin{gathered} m\angle3=m\angle1+m\angle2 \\ 7x+10=(3x+12)+(3x+18) \\ 7x+10=6x+30 \\ 7x-6x=30-10 \\ x=20 \end{gathered}$

With the value of x, we can calculate the measure of ∠3 as:

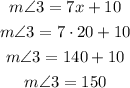
$\begin{gathered} m\angle3=7x+10 \\ m\angle3=7\cdot20+10 \\ m\angle3=140+10 \\ m\angle3=150\degree \end{gathered}$

Answer: m∠3 = 150°

Please log in or register to add a comment.