Let's imagine a point E in the line DA and at the left of point A.
From the formula to find the angle between a tangent and a chord:
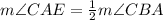
The measure of angle ABC is given: 220°. Then:
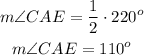
Now, from the figure, we can see that angles CAE and CAD form an angle of 180°. Then:
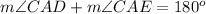
Replacing values and solving:
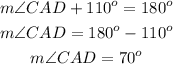
Then, finally, the measure of angle CAD is 70°.