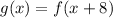We can see in the graph that f(x) and g(x) are parallel lines. This means that to transform f(x) into g(x), we can shift it horizontally or vertically.
Part A: Applying a vertical or horizontal shift to f(x) will result in g(x).
For part B, we need to find the transformations.
We can take two points of each function:
f(x): (0, -10) and (5, 0)
g(x): (0, 6) and (-3, 0)
Then, if we apply vertical shift in (0, -10), we should get the point (0, 6). Then, we can solve:
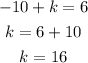
If we apply a horizontal shift, the point (5, 0) should transform into (-3, 0). Then:
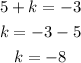
Part B:
Horizontal shift: k = -8
Vertical shift: k = 16
For part C we need to write an equation for each transformation.
Given a function h(x), a vertical shift of k units is written:
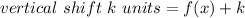
And a horizontal shift of k units:
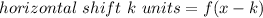
Vertical shift: This transformation adds 16 units in the y-coordinate.
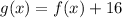
Horizontal shift: This transformation subtracts 8 from the x-coordinate: