Question

For a group of 160 students we know that:76 are taking a sequence course85 are taking an analysis course33 take sequence and analysis courses35 take courses in analysis and probability32 only take a sequence course15 take a sequence, probability and analysis courseIf each student takes at least one math class, how many are taking:a) A probability courseb) Sequence and probability lessons without analysisC) Only one course

Answer 1

Given:

The total number of students, N=160.

The number of students taking sequence course, n(S)=76.

The number of students taking analysis course, n(A)=85.

The number of students taking sequence and analysis courses , n(S∩A)=33.

The number of students taking analysis and probability courses, n(A∩P)=35.

The number of students taking sequence, analysis and probability courses, n(S∩A∩P)=15.

The number of students taking only sequence course, n(s)=32.

Since each student takes atleast one math course, the total number of students is,

`n(\text{S}\cup\text{A}\cup P)=N=160`

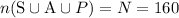
The venn diagram formula can be written as,

`n(\text{S}\cup\text{A}\cup P)=n(S)+n(A)+n(P)-n(S\cap A)-n(A\cap P)-n(S\cap P)+n(S\cap A\cap P)`

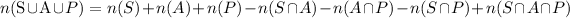
We use Venn diagram to solve the question. Let S represenst students taking sequence course, A represenst students taking analysis course and P represenst students taking probability course.

The students taking only analysis and sequence courses is,

`n\mleft(S\cap A\mright)-n\mleft(S\cap A\cap P\mright?)=33-15=18`

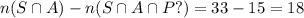
The students taking only analysis and probability courses is,

`n\mleft(A\cap P\mright)-n\mleft(S\cap A\cap P\mright)=35-15=20`

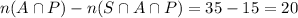
(b)

The students taking only sequence and probability lessons without analysis is,

`\begin{gathered} n(S\cup P)=n(S)-18-15-32 \\ =76-18-15-32 \\ =11 \end{gathered}`

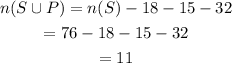
Hence, the number of students taking only sequence and probability lessons without analysis is 11.

(a)

Using the Venn diagram, the number of students taking only probability course is,

n(p)=160-32-18-11-15-32-20=32

Now, the number of students taking a probability course is,

n(P)=11+15+20+32=78.

Therefore, the number of students taking a probability course is 78.

(c)

The students that take only one course from the venn diagram is

N=32+32+32=96

Therefore, the students that take only one course is 96.