Question

Maria deposits $60000 into an account that pays 6% interest per year, compounded annually.John deposits $60000 into an account that also pays 6% per year. But it is simple interest.Find the interest Maria and John earn during each of the first three years.Then decide who earns more interest for each year.Assume there are no withdrawals and no additional deposits.

Answer 1

First year

For Maria we use

`A=P(1+r)^t`

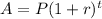
we have

`\begin{gathered} A=60,000(1+0.06)^1 \\ A=60,000(1.06) \\ A=63,600 \end{gathered}`

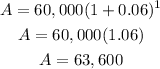
Interest becomes

`\begin{gathered} I=A-P \\ I=63,600-60,000= \\ =3,600 \end{gathered}`

For John we have

`\begin{gathered} I=(PRT)/(100) \\ =(60,000*6*1)/(100) \\ =3,600 \end{gathered}`

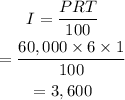
Hence in the First year, Marian erned $3,600 and John $3,600. so they earned same amount

Year 2

The amount for Maria in year 1 was $63,600, this becomes her principal in the second year. So we have

`\begin{gathered} A=P(1+r)^t \\ A=63,600(1+0.06)^1 \\ A=63,600*1.06 \\ A=67,416 \end{gathered}`

Interest becomes

`\begin{gathered} I=A-P \\ I=67,416-63,600 \\ =3,816 \end{gathered}`

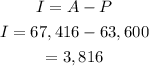
For John, we have

`\begin{gathered} I=(PRT)/(100) \\ I=(63,600*6*1)/(100) \\ =3,816 \end{gathered}`

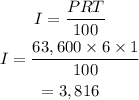
Hence in the 2nd year, Marian erned $3,816 and John $3,816. so they earned same amount

Year 3

The amount for Maria in year 2 was $67,416, this becomes her principal in the second year. So we have

`\begin{gathered} A=P(1+r)^t \\ A=67,416(1+0.06)^1 \\ A=67,416*1.06 \\ A=71,460.96 \end{gathered}`

Interest becomes

`\begin{gathered} I=A-P \\ I=71,460.96-67,416 \\ =4,044.96 \end{gathered}`

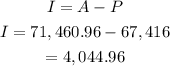
For John we have

`\begin{gathered} I=(PRT)/(100) \\ I=(71,460.96*6*1)/(100) \\ =4,287.66 \end{gathered}`

Hence in the 3rd year, Marian erned $4,044.96 and John $4,287.66

Hence John earns more