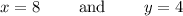Question

The equations 5x + 2y = 48 and 3x + 2y = 32 represent the money collected from school concert tickets sales during two class periods. If x represents the cost for each adult ticket and y represents the cost for each student ticket, find the values of x and y.x = 4 and y = 8x = 8 and y = 5x = 7 and y = 6x = 8 and y = 4

Answer 1

Notice that the coefficient of y is the same in both equations:

`\begin{gathered} 5x+2y=48 \\ 3x+2y=32 \end{gathered}`

Then, use the elimination method to solve the system of equations. Subtract the second equation from the first one:

`\begin{gathered} \Rightarrow(5x+2y)-(3x+2y)=48-32 \\ \\ \Rightarrow5x-3x+2y-2y=16 \\ \\ \Rightarrow2x=16 \\ \\ \Rightarrow x=(16)/(2) \\ \\ \therefore x=8 \end{gathered}`

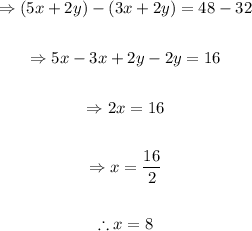
Replace x=8 in the first equation and solve for y:

`\begin{gathered} 5x+2y=48 \\ \\ \Rightarrow5(8)+2y=48 \\ \\ \Rightarrow40+2y=48 \\ \\ \Rightarrow2y=48-40 \\ \\ \Rightarrow2y=8 \\ \\ \Rightarrow y=(8)/(2) \\ \\ \therefore y=4 \end{gathered}`

Therefore, the solution to the system of equations is:

`x=8\qquad\text{ and }\qquad y=4`