We have the following:
We must pass each equation to the following form:

where m is the slope
when two lines are parallel the slopes are equal, when they are perpendicular they are inverse
therefore,
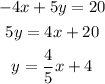
The slope is 4/5, the inverse is -5/4
now, for:
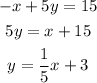
therefore, they are neither parallel nor perpendicular
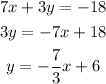
therefore, they are neither parallel nor perpendicular
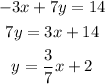
therefore, they are neither parallel nor perpendicular

therefore, they are neither parallel nor perpendicular
7x + 3y =-18 and - 3x + 7y = 14 are perpendicular