Question

One endpoint of a segment has coordinates (16,3). If the coordinates of the midpoint are (9,6), what are the coordinates of the other endpoint?

Answer 1

We know that

• One endpoint is (16,3).

,

• The midpoint is (9,6).

The formula for midpoint is

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))_{}`

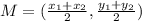
Where M is the midpoint. We replace the given endpoint and the midpoint.

`(9,6)=((16+x)/(2),(3+y)/(2))`

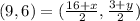
Now, we rewrite the equation by coordinates in order to find each variable.

`9=(16+x)/(2)`

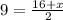
We multiply the equation by 2.

`\begin{gathered} 2\cdot9=2\cdot(16+x)/(2) \\ 18=16+x \end{gathered}`

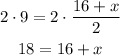
Then, we subtract 16 on each side.

`\begin{gathered} 18-16=16-16+x \\ x=2 \end{gathered}`

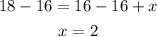
The x-coordinate of the other endpoint is 2.

Similarly, let's find y.

`6=(3+y)/(2)`

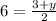
Multiply the equation by 2.

`\begin{gathered} 6\cdot2=(3+y)/(2)\cdot2 \\ 12=3+y \end{gathered}`

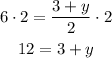
Then, subtract 3 on each side.

`\begin{gathered} 12-3=3-3+y \\ y=9 \end{gathered}`

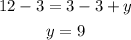
The y-coordinate of the other endpoint is 9.

Therefore, the other endpoint si (2, 9).