2. The surface area of a cylinder is given by the following formula:

Where pi=3.14, r is the radius r=d/2, and h is the height.
And the volume of a cylinder is given by:
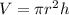
Where r is the radius r=d/2 and h is the height.
a. The given cylinder has a diameter d=18 cm (r = 18/2 = 9 cm) and a height h=7.5 cm.
Replace these values in the formulas and find the surface area and the volume:

The ratio of surface area to volume is then:
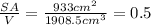
b. The given cylinder has a radius r = 5 cm and a height h=23 cm.
Replace these values in the formulas and find the surface area and the volume:
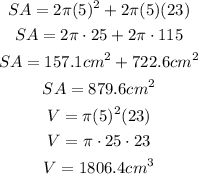
The ratio of surface area to volume is then:
