Question

A circle in the xy codirnate plane is represented by the equation X^2 + Y^2 - 6x = 11. what is the X- COORDINATE of the center circle

Answer 1

Given the equation of the circle:

`x^2+y^2-6x=11`

if we associate the terms with the variable x together, we have:

`(x^2-6x)+y^2=11`

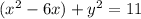
now, we can complete the square of the expression x^2-6x by dividing 6 by 2, and calculate the square of the result. In this case, we have:

`\begin{gathered} -(6)/(2)=-3 \\ \Rightarrow(-3)^2=9 \end{gathered}`

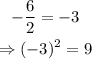
then, we have to add 9 on both sides of the equation to get the following:

`\begin{gathered} (x^2-6x+9)+y^2=11+9 \\ \Rightarrow(x-3)^2+y^2=20 \end{gathered}`

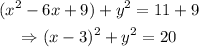
notice that the center of the circle is located at the point (h,k) = (3,0). Therefore, the x coordinate of the center of the circle is x = 3