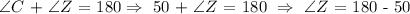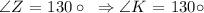Let's recall that in a parallelogram:
1. The opposite sides are paralell
In our exercise. sides CZ and KG are paralell. And so do sides KC and GZ.
2. Those opposite sides are equal in length.
3. The opposites angles are equal. In our exercise, angle C and G are equal and so do angles K and Z.
4. That also mean that the angles at the top of the figure are supplementary. It means they add up to 180 degrees. We have the same situation with the two angles at the bottom of the parallelogram.
In our case then:
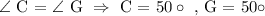
Now, we can find the measure of angles K and Z, as follows: