Answer: x = 1
Given:
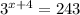
First, we need to express 243 as a number with base 3 raised to a certain exponent.
From this, if we take 3 to the fifth power, we will get the value of 243
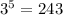
Now, we can rewrite the given equation as
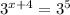
Now that we have the same base for both sides of the equation, we can now focus on solving the exponents for the value of x.
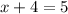
*Solve for x
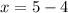
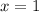
Therefore, the value of x = 1.
To check:
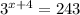
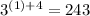
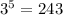
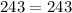
To check