Question

Use the data in the table below, which shows the employment status of individuals in a particular town by age group.A person from the town is randomly selected; what is the probability that the individual is employed full-time, given that he or sheis between 18 and 49 years of age?Full-timePart-timeUnemployed0-172416437118-2518520314826-34348652735-4958117911850+443162173

Answer 1

Given:

Given a table of data

Required: Probability that an individual is employed full time, given that he or she is between 18 and 49 years of age.

Step-by-step explanation:

Let A be the event " The individual is employed full time" and B be the event "He or she is between 18 and 49 years of age".

Then

`\begin{gathered} P(A)=\frac{\text{ Number of individuals employed full time}}{T\text{otal number of individuals}} \\ =(1581)/(3191) \end{gathered}`

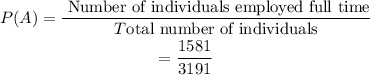
and

`\begin{gathered} P(B)=\frac{\text{ Number of individuals between the age 18 and 49}}{\text{ Total number of individuals}} \\ =(1854)/(3191) \end{gathered}`

Probability of individuals employed full time and aged between 18 and 49

`\begin{gathered} =P(A\cap B) \\ =(185+348+581)/(3191) \\ =(1114)/(3191) \end{gathered}`

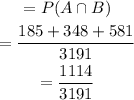
To find P(A/B).

By using the conditional probability,

`\begin{gathered} P(A|B)=(P(A\cap B))/(P(B)) \\ =(1114)/(1854) \end{gathered}`

Final Answer: Probability that an individual is employed full time, given that he or she is between 18 and 49 years of age is 1114/1854.