Question

I'm confused and I don't know how it works. Number 1.

Answer 1

1. The following formula is used to calculate the distance between two points:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2_{}}`

For this case you know that the points are:

`T(4,-2);U(-2,3)`

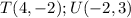
Then, you can set up that:

`\begin{gathered} x_2=-2 \\ x_1=4_{} \\ y_2=3 \\ y_1=-2 \end{gathered}`

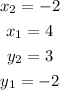
Then, you must substitute the corresponding coordinates into the formula and then evaluate, in order to find the distance between the points T and U (to the nearest tenth):

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2_{}} \\ d=\sqrt[]{(-2-4_{})^2+(3_{}-(-2)_{})^2_{}} \\ d=\sqrt[]{36+25} \\ d\approx7.8units \end{gathered}`

The answer is: Option c.