The chemical equation for this problem is:
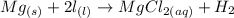
When the reaction between the metal and the acid is conducted in a eudiometer, the volume of the hydrogen gas produced can be easily determined. In the experiment described, magnesium metal will be reacted with an excess of hydrochloric acid and the volume of hydrogen gas produced at the experimental conditions will be determined.
According to Avogadros Law, the volume of 1 mole of any gas at STP (T = 273k and P = 1 atm) is 22.4L
Two important Gas Laws are required in order to convert the experimentally determined volume of hydrogen gas to that at STP. 1. Dalton’s law of partial pressures. 2. Combined gas law.
So we will find pressure of H2O first using Daltons law, and then we will use the combined gas law to find the volume of H2.
Daltons Law:
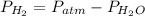
We need to know the vapour pressure of H2O
P H2O = P atm -P H2
For Trial 1:
mass of Mg = 0.043g
molar mass of Mg = 24,305 g/mol
number of moles of Mg = mass/molar mass
number of moles of Mg = 0.043g/24.305g/mol
n = 1.769x10^-3 mol
Now lets find the vapour pressure of H2O
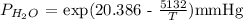
The temperature at trial 1 = 22.5 degrees C = 295.65 K T1
P H2O = exp (20.386 -(5132/295.65))mmHg
P H2O = 20.648 mmHg
Barometruc pressure is given = 765 mmHg
P H2 = 765 mmHg - 20.648 mmHg = 744.352 mmHg this is P1
Volume of H2 44.00 mL = 0.044 L this is V1
At STP: Pressure = 760 mm of Hg = P2
Temperature = 273 K = T2
So we need to solve for V2 using the following equation: The combined gas Law.
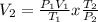
V2 = (744.352 x 0.044 x 273)/(295.65 x 760)
V2 = 0.0398 L
moles of H2 = 1.769x10^-3 mol
Therefore molar volume => 0.0398 L/1.769x10^-3 mol = 22.499 L/mol
For Trial 2:
mass of Mg = 0.042g
molar mass of Mg = 24,305 g/mol
number of moles of Mg = mass/molar mass
number of moles of Mg = 0.042g/24.305g/mol
n = 1.728x10^-3 mol
Now lets find the vapour pressure of H2O
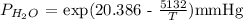
The temperature at trial 2 = 22.0 degrees C = 295.15 K T1
P H2O = exp (20.386 -(5132/295.15))mmHg
P H2O = 20.05 mmHg
Barometruc pressure is given = 765 mmHg
P H2 = 765 mmHg - 20.05 mmHg = 744.95 mmHg this is P1
Volume of H2 42.00 mL = 0.042 L this is V1
At STP: Pressure = 760 mm of Hg = P2
Temperature = 273 K = T2
So we need to solve for V2 using the following equation: The combined gas Law.
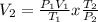
V2 = (744.95 x 0.042 x 273)/(295.15 x 760)
V2 = 0.0381 L
moles of H2 = 1.728x10^-3 mol
Therefore molar volume => 0.0381 L/1.728x10^-3 mol = 22.049 L/mol