Question

Given the piecewise functiong(x) = -343x, x= -2 (x-1)(x+ 2), x= -1 x³- x ² + 1, x ≠ -2, -1g(1) = ____

Answer 1

g(1) = 1

Step-by-step explanation:

Given the piecewise function:

`g(x)=\mleft\{\begin{aligned}-343x,\text{ x=-2} \\ (x-1)(x+2),\text{ x= -1} \\ x^3-x^2+1,\text{ x}\\e-2,\text{ -1}\end{aligned}\mright.`

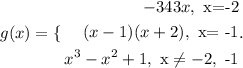
To find the value of g(1), this means x = 1

Looking at the piecewise function, the only function that satisfies the condition x = 1

is

`x^3-x^2+1`

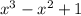
Because it is for all x different from -2 and -1, and x = 1 is.

Substituting x = 1 in

`x^3-x^2+1`

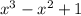
we have:

`\begin{gathered} 1^3-1^2+1 \\ \\ =1-1+1 \\ \\ =1 \end{gathered}`

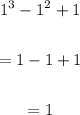
Therefore, g(1) = 1