Question

How to solve it and explain the the work to get the answer

Answer 1

Given,

`\bar{AB}\cong\bar{AE}`

Let ∠AB=∠AE=x

The sum of angle in a triangle=180°

Hence,

`x+x+24^0=180^0`
`\begin{gathered} 2x+24^0=180^0 \\ 2x=180^0-24^0 \\ 2x=156^0 \\ x=(156^0)/(2) \\ x=78^0 \end{gathered}`

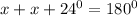
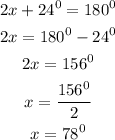
Let us get ∠ABC,

`\begin{gathered} \text{The sum of angles in a straight line=180}^0 \\ \angle ABC=180^0-x=180^0-78^0 \\ \angle ABC=102^0 \end{gathered}`

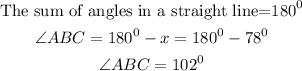
Let us get ∠BAD,

∠BAD is perpendicular to ∠EAB

`\begin{gathered} \angle BAD=90^0-24^0=66^0 \\ \angle BAD=66^0 \end{gathered}`

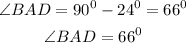
Let us now get ∠ADC,

The sum of angles in a quadrilateral is 360°.

`\angle ADC=360^0-(\angle ABC+\angle BAD+\angle BCD)`
`\begin{gathered} \angle ADC=360^0-(102^0+66^0+65^0) \\ \angle ADC=360^0-233^0 \\ \angle ADC=127^0 \end{gathered}`

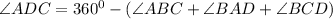
To solve for ∠CDF,

The sum of angles in a straight line is 180°.

`\begin{gathered} \angle CDF=180^0-\angle ADC \\ \angle CDF=180^0-127^0 \\ \angle CDF=53^0 \end{gathered}`

Hence, the m∠CDF is 53°.