Solution:
Given:
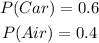
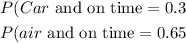
i) The probability that he arrives in Lagos early for the appointment is;
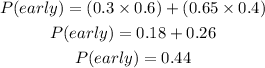
Therefore, the probability that he arrives in Lagos early for the appointment is 0.44
ii) The probability that he went by car if he arrived late for his appointment is;
To get the probability, we use conditional probability.
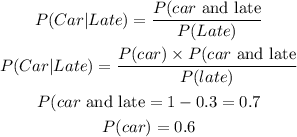
We now get the probability of late;
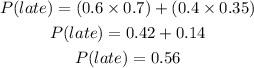
Therefore, the probability that he went by car if he arrived late for his appointment is;

Therefore, the probability that he went by car if he arrived late for his appointment is 0.75