Answer:
• Degree: 6
,
• Leading Coefficient: 2250
Explanation:
Given the function:
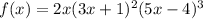
(a)Degree
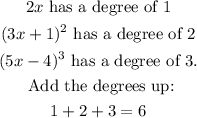
The degree of the function is 6.
(b)Leading Coefiicient
First, find the leading coefficient of each of the terms.
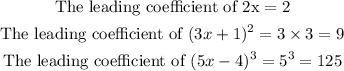
Multiply all the leading coefficients:

The leading coefficient is 2250.