Answer:
The measure of NQ is 32 units.
Step-by-step explanation:
Given that R is a midpoint of NP and S is a midpoint of PQ, the by the Midpoint Theorem for Triangles, we have:
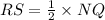
Substituting the given expressions, we have:
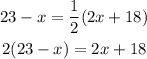
Next, solve for x:
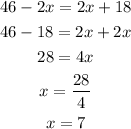
Thus, the measure of NQ will then be:
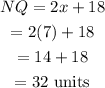
The measure of NQ is 32 units.