The mean and standard deviation of the scores are given below:
• Mean = 75
,
• Standard deviation = 4
We make use of the z-score formula below:
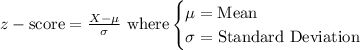
Part A (between 63 and 87)
First, we determine the z-scores.
![\begin{gathered} z-score=(63-75)/(4)=-(12)/(4)=-3 \\ z-score=(87-75)/(4)=(12)/(4)=3 \\ \text{From the z-score table: }P(-3<strong>Therefore, the percentage of scores that were between 63 and 87 is 99.73%.</strong><p>Part B (Above 83)</p>[tex]\begin{gathered} z-score=(83-75)/(4)=(8)/(4)=2 \\ \text{From the z-score table: }P(x>2)=0.02275 \end{gathered}]()
Therefore, the percentage of scores that were above 83 is 2.28%.
Part C (below 71)
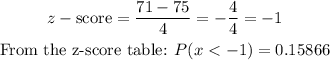
Therefore, the percentage of scores that were below 71 is 15.87%.
Part D (between 67 and 79)
[tex]\begin{gathered} z-score=\frac{67-75}{4}=\frac{-8}{4}=-2 \\ z-score=\frac{79-75}{4}=\frac{4}{4}=1 \\ \text{From the z-score table: }P(-2
Therefore, the percentage of scores that were between 67 and 79 is 81.86%.