The problem is essentially asking, how many ways can you select 6 different players from a group of 8 players?
When order is important, we use the permutation formula and when order is not important, we use the combination formula.
Here, the order is not important , so we use the combination formula. Shown below:
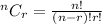
This is the number of ways to select r things from total n things.
We have
r = 6
n = 8
Substituting and simplifying, we have:
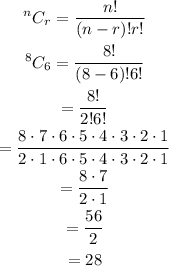
So,
Coach Malone would need 28 games to achieve his target.