Question

Let (-5,3) be a point on the terminal side of 0.Find the exact values of cost, and tan 0.

Answer 1

`\begin{gathered} \cos (\theta)=-0.858 \\ \csc (\theta)=1.93 \\ \tan (\theta)=-0.6 \\ \end{gathered}`

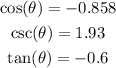
Step-by-step explanation: There is a point on the terminal side of some unknown angle "theta" provided the coordinates of this angle (-5,3), we need to determine the cos, csc, and tan of this angle". Visually this means:

Therefore the coordinates (-5,3) translate to:

`\begin{gathered} x=-5\rightarrow\text{ Adjacent} \\ y=3\rightarrow\text{ Opposite side} \\ \text{ } \end{gathered}`

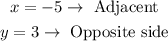
We have the adjacent and Opposite side, from this, we can calculate the hypotenuse using the "Pythagorean theorem" as follows, once we have the three sides of the triangle, then calculating the trigonometric rations would be the last simple step.

`\begin{gathered} a^2+b^2=c^2 \\ \therefore\rightarrow \\ c=\sqrt[]{a^2+b^2}\Rightarrow\sqrt[]{(-5)^2+(3)^2} \\ c=\sqrt[]{34}=5.83 \end{gathered}`

The final step, calculating cos csc and tan:

`\begin{gathered} \cos (\theta)=\frac{\text{ Adjacent}}{\text{Hypotenuse}} \\ \therefore\rightarrow \\ \cos (\theta)=(x)/(y)=(-5)/(5.83)=-0.858 \\ \cos (\theta)=-0.858 \\ ----------------- \\ \csc (\theta)=(1)/(\sin (\theta)) \\ \therefore\rightarrow \\ \sin (\theta)=\frac{\text{ Opposite}}{\text{hypotenuse}} \\ \sin (\theta)=(3)/(5.83) \\ \therefore\rightarrow \\ \csc (\theta)=((3)/(5.83))^(-1)=(5.83)/(3) \\ \csc (\theta)=(5.83)/(3)=1.93 \\ \csc (\theta)=1.93 \\ -------------------- \\ \tan (\theta)=\frac{\text{ Opposite}}{\text{Adjacent}} \\ \tan (\theta)=(3)/(-5)=-(3)/(5)=-0.6 \\ \tan (\theta)=-0.6 \end{gathered}`