Question

Consider the following function. Complete parts (a) through (e) below.y = - 2x2 + 4x+11***The parabola opens upward.b. Find the vertex.The vertex is (1,13).(Type an ordered pair.)c. Use the quadratic formula to find the x-intercepts.The x-intercept(s) is/are - 1.5,3.5.(Type an integer or a decimal rounded to the nearest tenth as needed. Use acomma to separate answers as needed.)d. Find the y-intercept. The y-intercept is(Type an integer or a fraction.)

Answer 1

Given:

`y=-2x^2+4x+11`

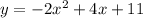
Required:

(a) Find parabola opens upward.

(b) Find the vertex.

(c) Find the X-intercepts.

(d) Find Y intercepts.

Step-by-step explanation:

The given equation is:

`y=-2x^(2)+4x+11`

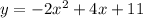
Rewrite it as:

`\begin{gathered} y=-2(x^2-2x)+11 \\ y=-2(x^2-2x+1)+11+2 \\ y=-2(x-1)^2+13 \end{gathered}`

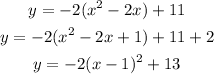
Compare the equation with the standard equation

`y=a(x-h)^2+k`

a = -2, h =1 and k =13

(a) Since the value of a = -2 < 0 so the parabola opens down.

(b) The vertex of the parabola is (h,k) .

Thus the vertex of given the parabola is (1, 13).

(c) At the X-intercept y = 0

`\begin{gathered} -2x^2+4x+11=0 \\ 2x^2-4x-11=0 \end{gathered}`

The given equation is a quadratic equation.

Compare it with

`ax^2+bx+c=0`

solve it as

`x=(-b\pm√(b^2-4ac))/(2a)`

(d) At the y-intercept x =0

`\begin{gathered} y=-2(0)^2+4(0)+11 \\ y=11 \end{gathered}`

Final Answer:

(a) Parabola opens downward

(b) vertex = (1, 13)

(d) y-intercept is 11