Question

Two barometers are made with water and mercury. Ifthe mercury column is 30 in. tall, how tall is the watercolumn?

Answer 1

We know that two barometers are measuring the same pressure when the mass in their columns are equal, that is, the two barometers will measure the same when:

`m_(Hg)=m_(H2O)`

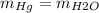
To find the mass of the barometer we need to remember that the mass is related to the density of the substance and its volume by:

`m=\rho V`

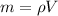
Hence the first equation takes the form:

`\rho_(Hg)V_(Hg)=\rho_(H2O)V_(H2O)`

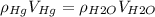
Now, let's assume the barometers are cylindrical, then their volume is given by:

`V=Ah`

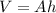
where A is the area of the base; let's further assume the area of the base is equal for both barometers; plugging this in our equation we have:

`\begin{gathered} \rho_(Hg)Ah_(Hg)=\rho_(H2O)Ah_(H2O)_{} \\ \rho_(Hg)h_(Hg)=\rho_(H2O)h_(H2O) \end{gathered}`

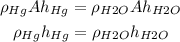
Hence we have the following equation relating the densities of the substances in the barometer and the height of the column in it:

`\rho_(Hg)h_(Hg)=\rho_(H2O)h_(H2O)`

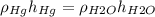
Now, before we plug the values of the densities we will convert the height of the mercury column to cm (this will make the operations easier), let's do that:

`30in\cdot(2.54cm)/(1in)=76.2cm`

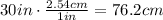
The density of mercury is 13.6 g/cm^3, the density of water is 1 g/cm^3; plugging the values we know we have that:

`\begin{gathered} (13.6)(76.2)=(1)h_(H2O) \\ h_(H2O)=1036.32 \end{gathered}`

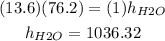
Hence, the height of the column of water is 1036.32 cm, let's convert this into inches:

`1036.32cm\cdot(1in)/(2.54cm)=408`

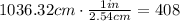
Therefore, the height of the column of water is 408 in tall.