Question

I’m not sure how to solve this problem it’s number 10 I’m in high school chemistry

Answer 1

The first step we have to follow is to convert the units of each of the measurements (mL to L, mmHg to atm and °C to K):

`\begin{gathered} 100mL\cdot(1L)/(1000mL)=0.1L \\ 688mmHg\cdot(1atm)/(760mmHg)=0.91atm \\ K=565+273.15=838.15K \end{gathered}`

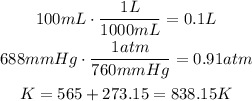
Now, use the ideal gases law to find the number of moles of carbon dioxide at these conditions:

`\begin{gathered} P\cdot V=n\cdot R\cdot T \\ n=\frac{P\cdot V_{}}{R\cdot T} \\ n=(0.91atm\cdot0.1L)/(0.082(atmL)/(molK)\cdot838.15K) \\ n=0.00132mol \end{gathered}`

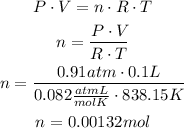
Now, use the chemical equation to find how many moles of acetic acid are needed to produce that amount of carbon dioxide:

`CH_3COOH+NaHCO_3\to CH_3COONa+CO_2+H_2O`

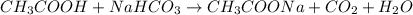
Use the stoichiometric ratio of moles of acetic acid used to moles of carbon dioxide produced:

`0.00132molCO_2\cdot(1molCH_3COOH)/(1molCO_2)=0.00132molCH_3COOH`

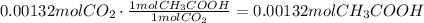
Use the molar mass of acetic acid to convert this amount of moles to mass:

`0.00132molCH_3COOH\cdot(60.1gCH_3COOH)/(1molCH_3COOH)=0.079gCH_3COOH`

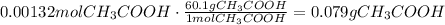
Finally use the density of acetic acid to find volume of 0.079g of this compound:

`0.079g\cdot(1ml)/(1.05g)=0.08292ml`

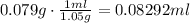
It means that 0.08292 would be needed to obtain the sample of carbon dioxide.