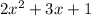Question

Subtract the rational expressions in simplest form. Is this correct?

Answer 1

The rational expression is given to be:

`(x-1)/(x+1)-(2x+3)/(2x+1)`

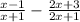
STEP 1: Find the Lowest Common Multiplier (LCM) of the denominators

`\text{LCM of }(x+1)\text{ and }(2x+1)\Rightarrow(x+1)(2x+1)`

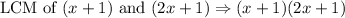
STEP 2: Adjust the fractions by dividing the LCM by the denominator of each fraction and multiplying the numerator and denominator by the result

`\begin{gathered} For\text{ }(x-1)/(x+1) \\ Multiplier=((x+1)(2x+1))/(x+1)=2x+1 \\ \text{New fraction:} \\ \Rightarrow((x-1)(2x+1))/((x+1)(2x+1)) \end{gathered}`

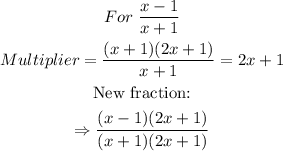
and

`\begin{gathered} For\text{ }(2x+3)/(2x+1) \\ Multiplier=((x+1)(2x+1))/(2x+1)=x+1 \\ \text{New fraction:} \\ \Rightarrow((2x+3)(x+1))/((2x+1)(x+1)) \end{gathered}`

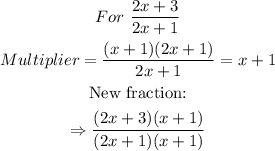
Hence, the expression becomes:

`\Rightarrow((x-1)(2x+1))/((x+1)(2x+1))-((2x+3)(x+1))/((2x+1)(x+1))`

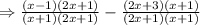
STEP 3: Apply the fraction rule

`(a)/(b)-(c)/(b)=(a-c)/(b)`

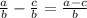
Hence, the expression becomes:

`\Rightarrow((x-1)(2x+1)-(2x+3)(x+1))/((x+1)(2x+1))`

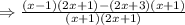
STEP 4: Expand and simplify the brackets using the FOIL method

`\mleft(a+b\mright)\mleft(c+d\mright)=ac+ad+bc+bd`

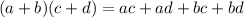
Hence, the expression becomes:

`\begin{gathered} \Rightarrow((2x^2+x-2x-1)-(2x^2+2x+3x+3))/(2x^2+x+2x+1) \\ \Rightarrow((2x^2-x-1)-(2x^2+5x+3))/(2x^2+3x+1) \\ \Rightarrow(2x^2-2x^2-x-5x-1-3)/(2x^2+3x+1) \\ \Rightarrow(-6x-4)/(2x^2+3x+1) \end{gathered}`

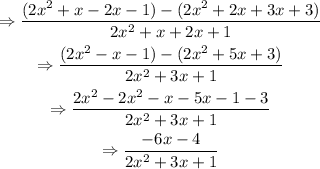
ANSWER:

The numerator is:

`-6x-4`

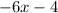
The denominator is:

`2x^2+3x+1`