The problem wants us to solve for the area of the window.
As we can see the window is in the form of a SQUARE shape with a measurement of 0.25 in for 1/2 the side of the window.
Since 1/2 of the side of the window is 0.25, the full measurement of its side is just times two of its half. Therefore:
Side = 0.25(2) = 0.5 in
And we can see at the bottom of the picture the word SCALE. The SCALE shows the relationship between the measurement of something (in our case a cabin) in a model to the measurement of that something in the real life.
In our case we have a scale of 1 in = 8 ft, it means that 1 inch in the paper is actually 8 feet in real life. Therefore the side of the window which measures 0.5 in. in the paper is actually 4 feet in real life. Because 0.5 inch is half of 1 inch and 4 feet is half of 8 feet. To show it mathematically we have:
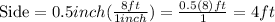
Since we now have a side of 4 ft. We can now solve for the area of our SQUARE WINDOW, using the formula of the area of the sqaure which is Area = Side x Side.
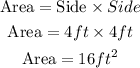
Therefore the area of the window is 16 square feet. LETTER C.