Question

Multiple Choice If m

Answer 1

Consider the image given below,

Since the diagonals of a kite are perpendicular, hence the angles at the center are 90 degrees.

Hence

From triangles of the shorter diagonals, triangle, ADC

`\angle DAE=\angle DCE\text{ (bases angles of isosceles triangle)}`

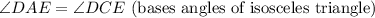
Then

`\begin{gathered} \angle ADE+\angle AED+\angle DAE=180^0(\text{ sum of angles in a triangle)} \\ \text{Where } \\ \angle ADE=48^0,\angle AED=90^0,\angle DAE=\angle DCE^{} \end{gathered}`

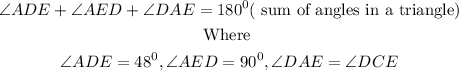
substituting the values we have

`\begin{gathered} 48^0+90^0+\angle DCE=180^0 \\ 138^0+\angle DCE=180^0 \end{gathered}`

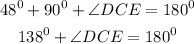
Then, subtracting 138 from both sides we have

`\begin{gathered} \angle DCE=180^0-138^0 \\ \angle DCE=42^0 \end{gathered}`

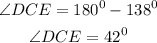
Hence

The measure of angle DCE= 42 degrees

Similarly, considering the triangle CAB

`\begin{gathered} \angle BCE=\angle BAE(\text{ base angle of an isosceles triangle )} \\ \text{Where } \\ \angle BCE=67^0 \end{gathered}`

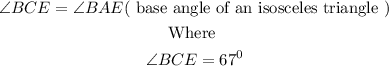
Then

`\angle BCE+\angle BAE+\angle ABC=180^0(\text{ sum fo angles in a triangle CAB)}`

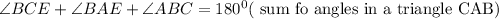
Hence

`\begin{gathered} 67^0+67^0+\angle ABC=180^0 \\ 134^0+\angle ABC=180^0 \end{gathered}`

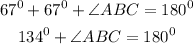
Subtracting 134 from both sides, we have

`\begin{gathered} \angle ABC=180^0-134^0 \\ \angle ABC=46^0 \end{gathered}`

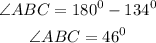
Hence

m < ABC =46°

Answer: m