Question

A colony of cats were introduced into a reserve. The number of cats present at timet(measured in years since the colony was introduced) on a certain reserve is given by the function12.31below. (Round your answers to the nearest whole number.) C =0.05 +0.56a. How many cats were initially on the reserve?catsb. Calculate C(10).C(10)=catsWrite a sentence explaining the meaning of the number you calculated below.C. Express the number of cats present after 17 years using functional notation.CLCalculate the number of cats present after 17 years.catsd. How much increase in the cat population do you expect from the 10th to the 17th year?cats

Answer 1

a) 12 cats

b) 232

c) 246

d) 14

Step-by-step explanation:

Given the expression for number of cats C present at time t:

`C\text{ = }\frac{12.31}{0.05+0.56^t^{}}`

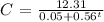
a) To find the number of cats initially on the reserve, let t = 0

Therefore, substitute 0 for t in the equation

`\begin{gathered} C\text{ = }(12.31)/(0.05+0.56^0) \\ \text{ = }\frac{12.31}{0.05\text{ + 1}} \\ \text{ = }(12.31)/(1.05) \\ =\text{ }11.72 \end{gathered}`

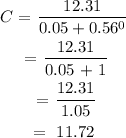
Number of cats initially on the reserve are approximately 12 cats

b) C(10):

`\begin{gathered} C(10)\text{ = }(12.31)/(0.05+0.56^(10))\text{ = 232.12} \\ \end{gathered}`

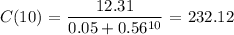
C(10) = 232

Here, C(10) means that C is a function of 10. This means at time = 10 years

C)Using function notation to express the number of cats present after 17 years, we have:

`C(17)\text{ = }(12.31)/(0.05+0.56^(17))`

`C(17)\text{ = }(12.31)/(0.05+0.56^(17))\text{ = }245.94`

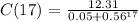
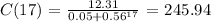
Therefore, number of cats present after 17 years are approximately 246 cats

C(17) = 246 cats

d) In this case, first find the number of cats present in the 10th year and subtract from the number of cats present in the 17th year.

`C(10)\text{ = }(12.31)/(0.05+0.56^(10))=\text{ }232.12`

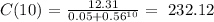
From question C above, we know C(17) = 246

Therefore, the increase in cat population to be expected from the 10th year to the 17th year is:

C(17) - C(10) = 246 - 232 = 14 cats