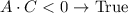Using the general equation of the conics we can analyze what type of conical section we can get:
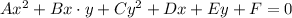
By changing the values of any of the constants, the shape of the corresponding conic will also change. For the case of the hyperbola
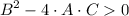
For this inequality to be fulfilled, we can guarantee that the second term is positive, since the second term is negative (-4AC), this must be less than zero, and by law of signs it becomes positive and the inequality is fulfilled.