a) The set of realizations of X can be given by the possible outcomes from the sum of two fair dice: {2,3,4,5,6,7,8,9,10,11,12}
b) If we consider (B,R) a possible outcomes from the blue and red dice, we have the following outcomes for every value for X:
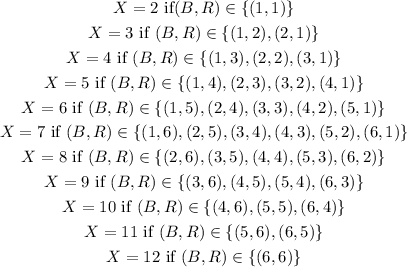
Therefore, the distribution of X, P(X) is given by the ratio between the number of possibilities for a given value of X and the total number of 36 combinations for (B,R)
Then we have:
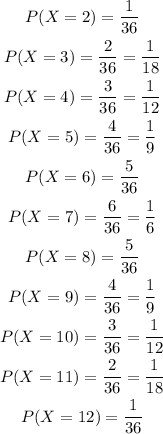
c)
The expected value for X is given by:
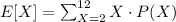
Based on the values obtained in part b, we have: