Question

Three machines A, B, and C produce 55%, 25% and 20% respectively. The percentages of defective output are 3.5%, 4.5% and 5.5%. If an item is selected randomly, find the probability that the item is defective.

Answer 1

We are given the following information concerning the three production machines;

`\begin{gathered} Of\text{ the total production;} \\ A=55\text{ \%}=0.55 \\ B=25\text{ \%}=0.25 \\ C=20\text{ \%}=0.20 \end{gathered}`

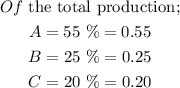
Also, we are given the percentage of defective output as follows;

`\begin{gathered} A=3.5\text{ \%}=0.035 \\ B=4.5\text{ \%}=0.045 \\ C=5.5\text{ \%}=0.055 \end{gathered}`

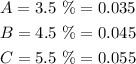
Therefore, if an item is selected randomly, the probability that the item is defective would be;

ANSWER:

The probability that the item is defective would be 0.0415